English

 

Η ιστορία του πολυσυζητημένου αριθμού e δεν μπορεί να ξεκινήσει, αν δεν γίνει πρώτα λόγος για τους λογαρίθμους.

Τον 16^ο – 17ο αιώνα παρατηρήθηκε μια σημαντική ανάπτυξη της επιστημονικής γνώσης σε όλους τους κλάδους. Οι ανακαλύψεις των νέων χωρών, ο γύρος του κόσμου από τον Μαγγελάνο και η ανάπτυξη του ναυτικού εμπορίου δημιούργησαν την ανάγκη παραγωγής χαρτών (Gerhard Mercator, 1596). Η εισβολή των μαθηματικών στην αστρονομία και στη φυσική μετά τον Κοπέρνικο, τον Γαλιλαίο και τον Κέπλερ καθώς και το πλήθος των δεδομένων που προέκυψαν προς επεξεργασία στις προαναφερόμενες επιστήμες, απαιτούσαν από τους επιστήμονες τη διεκπεραίωση περίπλοκων υπολογισμών. Έπρεπε να επινοηθούν τρόποι που θα τους απάλλασσαν από αυτό το βάρος. Και επειδή είναι ευκολότερο να προσθέτουμε παρά να πολλαπλασιάζουμε, βρέθηκε τρόπος μετατροπής της πρόσθεσης σε πολλαπλασιασμό , ο λογάριθμος.

 

O John Napier (1550-1617), 8^ος Λόρδος του Merchistoun στη Σκωτία, γνωστός για τα θρησκευτικού περιεχομένου βιβλία του, ήταν ο πρώτος που, δεχόμενος την πρόκληση μετατροπής μιας πράξης σε μια άλλη πιο απλή, παρατήρησε τη σχέση των όρων μιας γεωμετρικής προόδου και των αντίστοιχων εκθετών τους, που ακολουθούν αριθμητική πρόοδο.

Ο Napier παίρνοντας ως βάση τον αριθμό 1-10^-7 υποστήριξε ότι κάθε θετικός αριθμός Ν μπορεί να γραφεί ως Ν=10⁷(1-10^-7)^L.

Έτσι έχουμε τον πρώτο ορισμό του Νεπέριου λογάριθμου: L=Nap logΝ.

Επί 20 χρόνια συμπλήρωνε τους διαδοχικούς όρους της γεωμετρικής προόδου που κατασκεύασε συγκεντρώνοντας τους τελικά στο έργο του Mirifici Logarithmorum Canonis Descriptio.

Παρατήρηση: Εδώ εμφανίζεται και για πρώτη φορά η τιμή της ακολουθίας

όταν το ν είναι πάρα πολύ μεγάλο, ως βάση για λογαρίθμους.

 

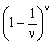
Το χρήμα είναι μαθηματικά

Τον 17^ο αιώνα κάποιος ανώνυμος έμπορος ή τοκογλύφος παρατήρησε μια παράξενη συμπεριφορά στην αύξηση του τόκου στις τραπεζικές συναλλαγές, που στηρίζονται σε ανατοκισμό με ετήσιο επιτόκιο διαιρεμένο σε ν ίσα μέρη, όταν ο αριθμός ν είναι πάρα πολύ μεγάλος. Ας παρακολουθήσουμε το φαινόμενο:

 

Η συνήθης τραπεζική μέθοδος αύξησης του δανειζόμενου κεφαλαίου είναι ο:

Ανατοκισμός

Έστω ότι καταθέτουμε € Κ σε ένα λογαριασμό που αποδίδει ε% ετήσιο επιτόκιο και ανατοκίζεται κάθε χρόνο.

Τέλος του 1^ου έτους: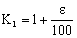

Τέλος του Ν^ου έτους: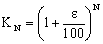

Άλλη συνήθης τραπεζική συναλλαγή είναι ο:

 

Ανατοκισμός ν φορές τον χρόνο με ετήσιο επιτόκιο διαιρεμένο σε ν ίσα μέρη

Δηλαδή, αν καταθέσουμε € 100 σε ένα λογαριασμό που αποδίδει 5% και τοκίζεται κάθε χρόνο:

 

Τέλος του 1^ου έτους: € 105,00

Αν καταθέτουμε €100 σε ένα λογαριασμό που αποδίδει 5% τον χρόνο και

ανατοκίζεται κάθε εξάμηνο σε ένα χρόνο ανατοκίζεται δύο (2) φορές με επιτόκιο 2,5%

Τέλος 1^ου έτους: 105,06

ανατοκίζεται κάθε τρίμηνο σε ένα χρόνο ανατοκίζεται τέσσερις (4) φορές με επιτόκιο 1,66%

Τέλος 1^ου έτους: 105,09 €

ανατοκίζεται κάθε μήνα σε ένα χρόνο ανατοκίζεται δώδεκα (12) φορές με επιτόκιο

0,416%.

Τέλος 1^ου έτους: 105,12 €

ανατοκίζεται κάθε ημέρα σε ένα χρόνο ανατοκίζεται τριακόσιες εξήντα

πέντε (365) φορές με επιτόκιο 0,0137 %

Τέλος 1^ου έτους: 105,19 €

 

Έστω ότι ο ανατοκισμός γίνεται ν φορές τον χρόνο. Για κάθε περίοδο μετατροπής ως επιτόκιο θεωρείται το ετήσιο επιτόκιο διαιρεμένο με τον ν, δηλαδή %.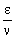

 

Τέλος 1^ου έτους: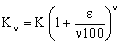

 

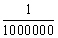
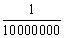
Παρατήρηση: Το τελικό κεφάλαιο για περίοδο μετατροπής πάρα πολύ μικρή, π.χ. / , δεν ξεπερνά το 2,72 του αρχικού κεφαλαίου.

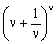
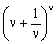
Παρατηρούμε ότι ο τύπος πλησιάζει μια τιμή χωρίς να τη φτάνει και αυτή είναι ο αριθμός e. Τότε λέμε ότι η ακολουθία με τύπο έχει όριο τον αριθμό e.

 

Το e ως όριο

Ο αριθμός e, όπως διαπιστώσαμε, είναι όριο της ακολουθίας.

Αλλά, αφού για μεγάλες τιμές του ν η τιμή του 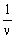θα είναι σχεδόν μηδέν,

έχουμε: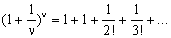

Συνεπώς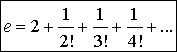

Ο τετραγωνισμός της υπερβολής

O Gregorius de Saint-Vincent (1584-1667), στην προσπάθεια τετραγωνισμού της υπερβολής, διαπιστώνει ότι, αν οι τετμημένες της γραφικής παράστασης της συνάρτησης μεταβάλλονται με γεωμετρική πρόοδο, τότε το εμβαδόν που βρίσκεται μεταξύ του άξονα των τετμημένων και της υπερβολής μεταβάλλεται με αριθμητική πρόοδο.

 

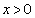
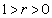
Έστω και

Αν οι τετμημένες

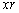
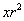
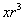
x, , , ...ακολουθούν γεωμετρική πρόοδο, τα εμβαδά

Ε1=1 – r ,

Ε1+E2=2(1 – r),

Ε1+E2+E3=3(1 – r) …ακολουθούν αριθμητική πρόοδο Προκύπτει λοιπόν το συμπέρασμα ότι το εμβαδό που βρίσκεται μεταξύ του άξονα των τετμημένων και της υπερβολής υπολογίζεται με τη βοήθεια της λογαριθμικής συνάρτησης.

 

Όταν το e συναντά το φ: Λογαριθμική έλικα

Ο Jacob Bernoulli (1654-1705) μελέτησε τη λογαριθμική έλικα και την ονόμασε spira mirabilis λόγω των σπανίων μαθηματικών ιδιοτήτων της, που την καθιστούν, μετά τον κύκλο, το πιο προσφιλές διακοσμητικό μοτίβο.

 

Η λογαριθμική έλικα περιγράφεται ως καμπύλη με αφετηρία ένα σημείο (τον πόλο) και ανελίσσεται με τρόπο ώστε η απόσταση των σημείων της από το πόλο να αυξάνει με γεωμετρική πρόοδο, εφόσον η γωνία περιστροφής αυξάνει με αριθμητική πρόοδο. Κάθε ευθεία που διέρχεται από τον πόλο τέμνει την έλικα υπό την ίδια γωνία.

 

Iconography

· Rick Reed, www.ps.missouri.edu/.../SlideRule02/index.html;

· www.educ.fc.ul.pt/docentes/opombo/seminario/neper/biografia.htm;

· www.nls.uk/scotlandspages/timeline/1614.html;

· http://en.wikipedia.org/wiki/File:Gr%C3%A9goire_de_Saint-Vincent_%281584-1667%29.jpg;

· http://cwx.prenhall.com/bookbind/pubbooks/thomas_br/chapter1/medialib/custom3/bios/bernoullijakob.htm;

· http://fridaysunset.net/creation/beauty.html;

· http://originalbeauty.wordpress.

com/2009/06/27/spirals-in-nature.

 

English